2.6 树与二叉树(共39题)
第1题:设某棵树的度为3,其中度为3,2,1的结点个数分别为3,0.4。则该树中的叶子结点数为()。
A、6
B、7
c、8
D、不可能有这样的树
参考解析:假设叶子结点个数为n。这棵树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为O的结点数,即为3+0+4+n。再根据树的性质:树的总的结点数为树中所有结点的度数之和再加1,则总结点数为3×3+2×0+1×4+OXn+1。3×3+1×4+1=3+4+n,则n=7,叶子结点数为7。本题答案为B选项。
第2题:设二叉树的前序序列为ABDEGHCFI,中序序列为DBGEHACIFJ。则按层次输出(从上到下,同一层从左到右)的序列为( )。
A、ABCDEFGHIJ
B、DGHEBIFCA
c、JIHGFEDCBA
D、GHIJDEFBCA
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)﹑后序遍历(访问根结点在访问左子树和访问右子树之后)。本题中二叉树的前序序列为ABDEGHCFIJ,可确定根结点为A,按层次输出(从上到下,同一层从左到右)时访问的第一个结点也应该是A,所以可排除B、C、D三项。本题答案为A选项。
第3题:某二叉树共有399个结点,其中有199个度为2的结点,则该二叉树中的叶子结点数为()。
A、不存在这样的二叉树
B、198
c、199
D、200
参考解析:根据二叉树的性质:对任何一棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。本题中,度为2的结点个数为199,贝叶子结点数为199+1=200。199+200=399,即这棵二叉树中只存在度为0和度为2的结点,不存在度为1的结点。本题答案为D选项。
第4题:循环队列的存储空间为Q(1:50)。经过一系列正常的入队与退队操作后,front=rear=25。后又成功地将一个元素入队,此时队列中的元素个数为( )。
A、1
B、50
c、26
D、2
参考解析∶设循环队列的存储空间为Q(1m),当front=rear=m时,循环队列为空;当front=rear且不等于m时,循环队列可能为空,也可能为满。当为空时,可以插入元素;当为满时,插入元素会发生“上溢”错误。题目中已经说明“成功地将一个元素入队”,说明之前循环队列的状态为空,插入一个元素后,队列中共有1个元素。本题答案为A选项。
第5题:设二叉树的前序序列为ABCDEF,中序序列为ABCDEF,则该二叉树的后序序列为()。
A、ABCDEF
B、FEDCBA
c、DEFCBA
D、CBAFED
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)﹑后序遍历(访问根结点在访问左子树和访问右子树之后)。本题中,二叉树的前序序列为ABCDEF,可确定二叉树的根结点为A,由于后序序列最后访问根结点,可排除A、D两项;由中序序列为ABCDEF可知,以.A为根的这棵二叉树不存在左子树,且由前序序列和中序序列相同可判断出每棵子树均不存在左子树(即只有右子树),后序序列先访问处于右子树上的结点F。本题答案为B选项。
第6题:设二叉树共有375个结点,其中度为2的结点有187个。则度为1的结点个数是()。
A、不可能有这样的二叉树
B、1
c、188
D、0
参考解析:对任何一棵二叉树,度为O的结点(即叶子结点)总是比度为2的结点多一个。本题中,度为2的结点个数为187,则度为0的结点个数为187+1=188,则度为1的结点个数为375-187-188=0。本题答案为D选项。
第7题:某完全二叉树按层次输出(同一层从左到右)的序列为ABCDEFGH。该完全二叉树的前序序列为( ) 。
A、ABCDEFGH
B、ABDHECFG
c、HDBEAFCG
D、HDEBFGCA
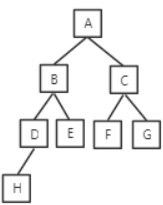
参考解析:完全二叉树是指除最后一层外,每一层上的节点数均达到最大值,在最后一层上只缺少右边的若干结点。本题中,完全二叉树按层次输出)(同一层从左到右)的序列为ABCDEFGH,则这棵二叉树如下图所示,其前序序列为
ABDHECFG。本题答案为B选项。
第8题:在具有2n个结点的完全二叉树中,叶子结点个数为( )。
A、n-1
B、n
c、n+1
D、n/2
参考解析:对任何一棵二叉树,度为O的结点(即叶子结点)总是比度为2的结点多一个。在完全二叉树中,只在最后一层上缺少右边的若干结点,所以度为1的结点个数为0或1。假设度为2的结点个数为x,则叶子结点个数为x+1。若度为1的结点个数为0,x+x+1+0无法和2n相等,不存在这样的二叉树,则度为1的结点个数为1,x+X+1+1=2n, x=n-1,所以叶子结点个数为n。本题答案为B选项。
第9题:设二叉树的后序序列与中序序列均为ABCDEFGH,则该二叉树的前序序列为()。
A、HGFEDCBA
B、ABCDEFGH
c、ABCDHGFE
D、DCBAHGFE
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后)。本题中,二叉树的后序序列为ABCDEFGH,可确定该二叉树的根结点为H,由于前序序列首先要访问根结点H,可直接排除B、C、D三项。本题答案为A选项。
第10题:设非空二叉树的所有子树中,其左子树上的结点值均小于根结点值,而右子树上的结点值均不小于根结点值,则称该二叉树为排序二叉树。对排序二叉树的遍历结果为有序序列的是( )。
A、前序序列
B、中序序列
c、后序序列
D、前序序列或后序序列
参考解析:在该二叉树中,左子树上的结点值均小于根结点值,右子树上的结点值均不小于根结点值,要使遍历结果为有序序列贝需先遍历左子树,再遍历根结点,最后遍历右子树,即为中序遍历序列。本题答案为B选项。
第11题:度为3的一棵树共有30个结点,其中度为3,1的结点个数分别为3,4。则该树中的叶子结点数为
A、15
B、16
c、14
D、不可能有这样的树
参考解析:假设叶子结点个数为m,度为2的结点个数为n。由树的总的结点数为树中所有结点的度数之和再加1,则
3×3+2Xn+1×4+0×m+1=30,n=8,即度为2的结点个数为8。树的总的结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,则3+8+4+m=30,m=15,即叶子结点数为15。本题答案为A选项。
第12题:设二叉树中有20个叶子结点,5个度为1的结点,则该二叉树中总的结点数为()。
A、45
B、46
c、44
D、不可能有这样的二叉树
参考解析:对任何一棵二叉树,度为O的结点(即叶子结点)总是比度为2的结点多一个。叶子结点个数为20,则度为2的结点个数为20-1=19。该二叉树的总的结点数为19+5+20=44。本题答案为C选项。
第13题:设一棵树的度为3,其中没有度为2的结点,且叶子结点数为6。该树中度为3的结点数为()。
A、不可能有这样的树
B、1
c、2
D、3
参考解析:假设度为3的结点数为x,度为1的结点数为y。树的总的结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为x+0+y+6。再根据树的总的结点数为树中所有结点的度数之和再加1,则总结点数为
3×x+2×0+1xy+0×6+1。3xx+y+1=x+y+6,则x=2.5,结点个数不可能为小数,所以不可能有这样的树。本题答案为A选项。
第14题:设一棵树的度为3,其中没有度为2的结点,且叶子结点数为5。该树中度为3的结点数为()。
A、1
B、2
c、3
D、不可能有这样的树
参考解析:设度为3的结点数为x,度为1的结点数为y,则树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为x+0+y+5。再根据树的总结点数为树中所有结点的度数之和再加1,则总结点数为
3×X+2x0+1×y+0×5+1。x+y+5=3xx+y+1,则x=2,所以度为3的结点个数为2。本题答案为B选项。
第15题:设二叉树的前序序列与中序序列均为ABCDEFGH,则该二叉树的后序序列为()。
A、ABCDEFGH
B、ABCDHGFE
c、DCBAHGFE
D、HGFEDCBA
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,二叉树的前序序列与中序序列均为ABCDEFGH,可确定该二叉树的根结点丙A且结点A没有左子树,后序序列最后访问的是根结点A,只有D项满足。本题答案为D选项。
第16题:某完全二叉树按层次输出(同一层从左到右)的序列为ABCDEFGH。该完全二叉树的中序序列为( ) 。
A、ABDHECFG
B、ABCDEFGH
c、HDBEAFCG
D、HDEBFGCA
参考解析:完全二叉树是指除最后一层外,每一层上的节点数均达到最大值,在最后一层上只缺少右边的若干节点。完全二叉树按层次输出的序列为ABCDEFGH,则二叉树如下图所示。该二叉树的中序序列为HDBEAFCG。本题答案为C选项。
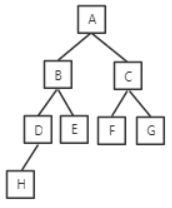
第17题:下列叙述中正确的是( )。
A、多重链表必定是非线性结构
B、任何二叉树只能采用链式存储结构
C、排序二叉树的中序遍历序列是有序序列
D、堆可以用完全二叉树表示,其中序遍历序列是有序序列
参考解析:结点中具有多个指针域的链表就称为多重链表,双向链表有两个指针域,属于线性结构,A选项错误。在二叉树中,满二叉树与完全二叉树可以按层次进行顺序存储,B选项错误。设非空二叉树的所有子树中,其左子树上的结点值均小于根结点值,而右子树上的结点值均不小于根结点值,则称该二叉树为排序二叉树。对排序序列进行中序遍历,遍历结果为有序序列,C选项正确。若有n个元素的序列,将元素按顺序组成一棵完全二叉树,当且仅当满足条件①:根结点值大于等于左子树的结点值且大于等于右子树的结点值,或条件②:根结点值小子等于左子树的结点值且不于等于右子树的结点值时称为堆。堆的左子树的结点值与右子树的结点值大小无法确定,所以对堆进行中序遍历无法确定是否为有序序列,D选项错误。本题答案为C选项。
第18题:设二叉树的前序序列为ABCDEF,中序序列为BDFECA,则该二叉树的深度为(根结点为第1层)( ) 。
A、2
B、3
c、4
D、6
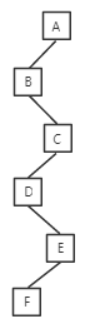
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。二叉树的前序序列为ABCDEF,可确定这棵二叉树的根结点为A中序序列为BDFECA,可确定根结点A没有右子树,结点B没有左子树,结点B的右子树的根结点为C。按照同样的原理来分析以C为根结点的子树,其前序序列为CDEF,中序序列为DFEC,可知结点C没有右子树;再继续分析下去,结点D没有左子树,结点E没有右子树,结点F为叶子结点。该二叉树如下图所示,则二叉树的深度为6。本题答案为D选项。
第19题:设某树的度为3,且度为3的结点数为5,度为2的结点数为4,没有度为1的结点。则该树中的叶子结点数为( )。
A、12
B、15
C、24
D、不可能有这样的树
参考解析︰假设叶子结点个数为n。树的总的结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为5+4+0+n。再根据树的总的结点数为树中所有结点的度数之和再加1,则总结点数为3×5+2x4+1×0+0×n+1。
3×5+2x4+1=5+4+n,则n=15,叶子结点数为15。本题答案为B选项。
第20题:下列叙述中正确的是( )。
A、向量是顺序存储的线性结构
B、只有一个根结点和一个叶子结点的结构必定是线性结构
c、非线性结构只能采用链式存储结构
D、所有非线性结构都能采用顺序存储结构
参考解析:只有一个根结点和一个叶子结点的数据结构可以是树结构(非线性结构),所以只有两个结点无法确定是否为线性结构,B选项叙述错误。二叉树属于非线性结构,满二叉树与完全二叉树可以按层次进行顺序存储,C选项叙述错误。只有部分非线性结构可以采用顺序存储,D选项叙述错误。本题答案为A选项。
第21题:设二叉树的前序序列为ABCDEF,中序序列为BDFECA,则该二叉树的后序序列为()。
A、FEDCBA
B、ABCDEF
C、BDFECA
D、CBAFED
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。二叉树的前序序列为ABCDEF,可确定这棵二叉树的根结点为A,在后序遍历中最后访问结点A,因此排除B、D两项。中序序列为BDFECA,则结点A不存在右子树,在对以结点B为根结点进行后序遍历时,最后访问的肯定是B结点,因此排除C项。本题答案为A选项。
第22题:某棵树中共有25个结点,且只有度为3的结点和叶子结点,其中叶子结点有7个,则该树中度为3的结点数为( )。
A、7
B、8
c、6
D、不存在这样的树
参考解析:树的结点数为25,只有度为3的结点和叶子结点,其中叶子结点有7个,则按照题意度为3的结点数为25-7=18。由于树中的结点数为树中所有结点的度数之和再加1,则树的总的结点数为3×18+1=55,与题目矛盾,所以不存在这样的树。本题答案为D选项。
第23题:某二叉树的前序序列为ABDFHCEG,中序序列为HFDBACEG。该二叉树的后序序列为()。
A、HFDBGECA
B、ABCDEFGH
c、HGFEDCBA
D、ACEGBDFH
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,二叉树的前序序列为ABDFHCEG,可确定该二叉树的根结点为A,后序序列最后访问的肯定是根结点A,排除B、D两项。再根据中序序列为HDBACEG,可确定结点A的左子树的根结点是B,右子树的根结点是C,则后序序列倒数第2个访问的肯定是结点C,排除C选项。本题答案为A选项。
第24题,某二叉树的后序遍历序列与中序遍历序列相同,均为ABCDEF,则按层次输出(同一层从左到右)的序列为( )。
A、ABCDEF
B、CBAFED
C、FEDCBA
D、DEFCBA
参考解析:二叉树遍历可以分为3种:前序遍历(访问根结点在访问左子树和访问右子树之前)、中序遍历(访问根结点在访问左子树和访问右子树两者之间)、后序遍历(访问根结点在访问左子树和访问右子树之后),并且在遍历左右子树时也遵循同样的规则。本题中,后序遍历序列与中序遍历序列习为ABCDE,可确定该二叉树的根结点为F,且每个结点均不存在右子树,因此按层次输出的序列应为FEDCBA。本题答案为C选项。
第25题:设一棵树的度为4,其中度为4,3,2,1的结点个数分别为2,3,3,0。则该棵树中的叶子结点数为( )。
A、15
B、16
c、17
D、不可能有这样的树
参考解析∶假设叶子结点个数为n。度为4的树的总结点数为度为4的结点数+度为3的结点数+度为2的结点数+度为1的结点数+度为O的结点数,即为2+3+3+0+n。再根据树的总的结点数为树中所有结点的度数之和再加1,则总结点数为
4×2+3×3+2x3+1×0+0×n+1。4x2+3x3+2x3+1=2+3+3+n,则n=16,叶子结点数为16。本题答案为B选项。
第26题:设一棵树的度为3,其中度为3,2,1的结点个数分别为4,1,3。则该棵树中的叶子结点数为( )。
A、10
B、11
c、12
D、不可能有这样的树
参考解析:假设叶子结点个数为n。树的总结点数为度为3的结点数+度为2的结点数+度为1的结点数+度为0的结点数,即为4+1+3+n。再根据树的总结点数为树中所有结点的度数之和再加1,则总结点数为3×4+2×1+1×3+0×n+1。
3x4+2×1+1×3+1=4+1+3+n,则n=10,叶子结点数为10。本题答案为A选项。
第27题:某二叉树有49个度为2的结点,4个度为1的结点,则( )。
A、该二叉树共有103个结点
B、该二叉树的结点数不确定
c、该二叉树共有101个结点
D、不可能有这样的二叉树
参考解析:对任何一棵二叉树,度为O的结点(即叶子结点)总是比度为2的结点多一个。本题中,度为2的结点个数为49,则度为0的结点个数为49+1=50。二叉树的总结点数等于度为2的结点数+度为1的结点数+度为O的结点数,则该二叉树的总结点数为49+4+50=103。本题答案为A选项。
第28题:某二叉树有49个度为2的结点,4个度为1的结点,30个叶子结点,则( )。
A、该二叉树只能有83个结点
B、这样的二叉树不惟一
c、该二叉树共有103个结点
D、不可能有这样的二叉树
参考解析:二叉树具有如下性质:对任何一棵二叉树,度为O的结点(即叶子结点)总是比度为2的结点多一个。本题中,度为2的结点个数为49,度为0的结点个数为30,不符合二叉树的基本性质,不可能有这样的二叉树。本题答案为D选项。
第29题:某完全二叉树有256个结点,则该二叉树的深度为( )。
A、7
B、8
c、9
D、10
参考解析:二叉树的基本性质:深度为K的二叉树中,最多有2k-1个节点。28-1<256<29-1,则该完全二叉树的深度为9。本题答案为C选项。
第30题:某二叉树的深度为7,其中有64个叶子结点,则该二叉树中度为1的结点数为( )。
A、0
B、1
c、2
D、63
参考解析∶在深度为K的二叉树中,最多有2K-1个结点。该二叉树的深度为7,则该二叉树最多有27-1=127个结点。对任何-棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。该二叉树中叶子结点个数为64,则度为2的结点个数为63。假设该二叉树的总结点数为n(n<=127),则度为1的结点数为n-64-63,n最大为127,则度为1的结点个数为0。本题答案为A选项。
第31题,在具有n个结点的二叉树中,如果各结点值互不相同,但前序遍历序列与中序遍历序列相同,则该二叉树的深度为(根结点在第1层)( )。
A、n-1
B、n/2+1
c、n
D、n+1
参考解析∶若二叉树的前序遍历序列与中序遍历序列相同,则二叉树中任意一个结点均不存在左子树﹔若二叉树的后序遍历序列与中序遍历序列相同,则二叉树中任意一个结点均不存在右子树。该二叉树具有n个结点,则该二叉树的深度为n。本题笞案为C选项。
第32题:对如下图所示的二叉树进行前序遍历的结果为( )。
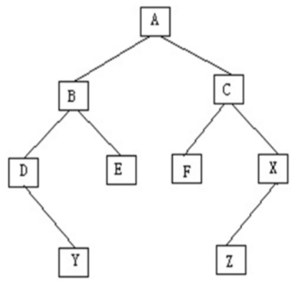
A、DYBEAFCZX
B、YDEBFZXCA
C、ABDYECFXZ
D、ABCDEFXYZ
参考解析:前序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中,首先访问根结点,然后遍历左子树,最后遍历右子树;并且在遍历左右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。本题中,二叉树的根结点是A,因此前序遍历首先访问结点A,排除A、B两项;然后再前序遍历左子树的各个结点,最后前序遍历右子树上的各个结点,访问完结点B后,访问结点D,排除D项。本题答案为C选项。
第33题:某二叉树共有12个结点,其中叶子结点只有1个。则该二叉树的深度为(根结点在第1层)()。
A、3
B、6
c、8
D、12
参考解析:对任何一棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。本题中,叶子结点个数为1,则度为2的结点个数为O,所以该二叉树只存在度为1的结点和叶子结点。度为1的结点个数为12-1=11,则该二叉树的深度为12。本题答案为D选项。
第34题:深度为7的二叉树共有127个结点,则下列说法中错误的是( )。
A、该二叉树有一个度为1的结点
B、该二叉树是满二叉树
c、该二叉树是完全二叉树
D、该二叉树有64个叶子结点
参考解析:深度为K的二叉树中,最多有2K-1个节点。深度为7的二叉树最多有27-1=127。深度为7的二叉树共有127个结点,则该二叉树为满二叉树,B选项正确。满二叉树一定是完全二叉树,C选项正确。在满二叉树中,只有度为2和度为0的结点,没有度为1的结点,A选项错误。度为o的结点(叶子结点)位于第7层,结点个数为27-1=26=64,D选项正确。本题答案为A选项。
第35题:深度为7的完全二叉树中共有125个结点,则该完全二叉树中的叶子结点数为()。
A、62
B、63
c、64
D、65
参考解析:完全二叉树指除最后一层外,每一层上的结点数均达到最大值,在最后一层上只缺少右边的若千结点。本题中,完全二叉树的深度为7,则前6层是深度为6的满二叉树,前6层的结点数为26-1=63,则全二叉树在第7层共有125-63=62个叶子结点。在第6层的结点个数为26-1=32,因为第7层只有62个叶子结点,则第6层有1个结点没有左右子树,属于叶子结点,该完全二叉树共有62+1=63个叶子结点。本题答案为B选项。
第36题:下列叙述中正确的是( )。
A、多重链表一定是非线性结构
B、顺序存储结构一定是线性结构
c、有的二叉树也能用顺序存储结构表示
D、有两个指针域的链表就是二叉链表
参考解析∶在计算机中,二叉树属于非线性结构,通常采用链式存储,但对于满二叉树和完全二叉树来说,也可以按层次进行顺序存储,因此B选项错误、C选项正确。双向链表中结点有两个指针域,但双向链表属于线性结构,不属于二叉链表,A、D两项错误。本题答案为C选项。
第37题:下列关于二叉树的叙述中,正确的是( ) .
A、叶子结点总是比度为2的结点少一个
B、叶子结点总是比度为2的结点多一个
c、叶子结点数是度为2的结点数的两倍
D、度为2的结点数是度为1的结点数的两倍
参考解析:对任何一棵二叉树,度为0的结点(即叶子结点)总是比度为2的结点多一个。本题答案为B选项。
第38题:下列结构中属于非线性结构的是( )。
A、循环队列
B、二维数组
c、二叉链表
D、双向链表
参考解析:二叉树的链式存储结构称为二叉链表,二叉树是一种非线性结构,所以二叉链表属于非线性结构。本题答案为C选项。
第39题:深度为5的完全二叉树的结点数不可能是( )。
A、15
B、16
c、17
D、18
参考解析:完全二叉树是指除最后一层外,每一层上的节点数均达到最大值,在最后一层上只缺少右边的若干结点。深度为4的满二叉树的结点数为24-1=15,深度为5的满二叉树的结点数为25-1=31,所以深度为5的完全二叉树的结点数应大于15且小于等于31。本题答案为A选项。