1.2.1 进位计数制
1.2.1 进位计数制
数制(Number System)也称为计数制,是指用一组固定的数字符号和统一的规则来表示数值的方法。按进位的方法进行计数,称为进位计数制。在日常生活和计算机中采用的都是进位计数制。
在进位计数制中有三个基本要素:数位、基数和位权。数位是指数码在一个数中所处的位置;基数是指在某种数制中所能使用的数码的个数,例如十进制数中,每个数位上可以使用0~9中任一数字,其基数为10;位权等于某数制的基数的次方。每个数位上的数码所表示的数值大小,等于这个数位上的数码乘上位权。数码所在的位置不同,所对应的位权也不同。例如十进制数中,小数点左边的第一位的位权为100,左边第二位的位权为101,左边第三位的位权为102,依此类推。
进位计数制很多,这里主要介绍与计算机技术有关的几种常用进位计数制。在微机中,一般在数字的后面用特定字母表示该数的进制。例如:B(二进制)、D(十进制,D可省略)、O(八进制)、H(十六进制)等。
◆ 十进制:具有10个不同的数码符号0、1、2、3、4、5、6、7、8、9,其基数为10,十进制数的特点是逢十进一。例如:(2137)D=2×103+1×102+3×101+7×100。
◆ 二进制:具有2个不同的数码符号0和1,其基数为2,二进制数的特点是逢二进一。例如:(1011)B=1×23+0×22+1×21+1×20=(11)D 。
◆ 八进制:具有8个不同的数码符号0、1、2、3、4、5、6、7,其基数为8,八进制数的特点是逢八进一。例如:(1162)O=1×83+1×82+6×81+2×80=(626)D 。
◆ 十六进制:具有16个不同的数码符号0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F,其基数为16,十六进制数的特点是逢十六进一。例如:(2BF)H=2×162 +11×161+15×160=(703)D 。
从上面的例子可以看出,同一数值在不同的进制中的表示结果是不一样的。表1-1列出了十进制数0~15在不同进制中的表示方法。
表1-1 不同进制间的表示方法
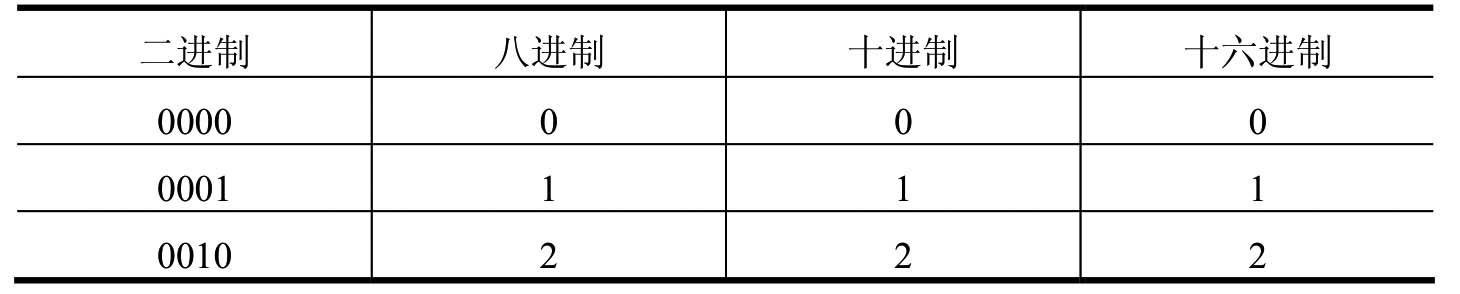
(续表)