三、结构方程模型分析
三、结构方程模型分析
结构方程模型也叫潜变量模型,是一种多元统计建模分析方法。结构方程分析可用来同时处理多个因变量,并可比较及评价不同的理论模型。在结构方程模型中,我们可以提出一个特定的因子结构,检验它是否和数据吻合。也可进行结构方程的多组分析,比较各组别内的关系是否能够保持不变,各因子的均值是否具有显著差别(侯杰泰、温忠麟、成子娟,2004)[24]。
(一)样本数要求和数据输入
在分析结构方程之前,应检查样本数是否符合进行分析的要求。Anderson 和Gerbing(1988)认为100-150是最低标准;Shumacker和Lomax(1996)认为样本容量在200-500间比较合适;Marsh,Hau,Balla和Grayson(1998)以及Marsh和Hau(1999)证实如果观察变量和因子数之比为3或4,则样本量至少为100,如果该比值大于或等于6,则只需要50个样本就足够了;Bentler和Chou(1987)指出:如果变量成正态分布,则每个变量配5个样本足够,如果是其他分布,则每个变量需要10个样本;Bagozzi(1980)认为,样本数减去待估计的参数个数应大于50;如果是采用极大似然法来估计,样本数最少应该在100-150之间(Ding, Velicer, and Harlow, 1995)。本研究的样本容量为113,符合要求。
(二)结构方程模型的评价
本研究将用结构方程模型来检验各变量间的关系,并了解企业的所有权、产业性质、企业所在地理区域等背景变量对模型变量关系的影响。研究中将用结构方程模型的分析软件LISREL8.70,进行数据的分析处理,用最大似然法(ML)对模型参数进行估计,而且将根据Bagozzi & Yi(1988)提出的模型评估的三个标准:基本拟合标准(preliminary fit criteria)、整体模型拟合优度(overall model fit)、模型内在结构拟合优度(fit of internal structure of model)三个方面评价模型的拟合度。基本要求如下:
1.基本拟合标准
该标准用于检验模型的误差和是否存在误输入的情况,通常从以下四个方面来检验。
(1)不能有负的测量误差;
(2)测量误差必须具有显著性;
(3)因子载荷值必须在0.5~0.9之间;
(4)不能有很大的标准误差。
2.整体模型拟合优度
整体模型拟合优度用来评价模型与数据的适配程度,通常用三类指标描述:
(1)绝对拟合度
绝对拟合度(absolute fit measures)是将理论模型(Mt)和饱和模型(Ms)[25]比较得到的一个统计量,常用的衡量指标有卡方统计值(x2)、近似误差均方根(Root Mean Square Error of Approximation,RMSEA)、标准化残差均方根(Standardized Root Mean square Residual, SRMR)、拟合优度指数(Goodness of Fit Index, GFI)、修正的拟合优度指数(Adjusted Goodness of Fit Index, AGFI)四种指标。Hu & Bentler(1995)认为四种指标在不同的情况下各有误差存在,侯杰泰等(2004)认为其中,RMSEA受样本数量N的影响较小,是较好的绝对拟合指标。
(2)相对拟合度
相对拟合度(comparative fit measures)是通过将理论模型(Mt)与基准模型(baseline model)[26]比较得到的统计量。简单地说,相对拟合指数是将理论模型与虚模型进行比较,考察拟合程度改进了多少。常用的衡量指标有基准拟合指数(Normed Fit Index,NFI)、调整的基准拟合指数(Non-normed Fit Index, NNFI)、相对拟合指数(Comparative Fit Index, CFI)等。
(3)简约拟合度
简约拟合度(parsimony fit indices)是在拟合指数中引入简约原则,以惩罚参数多的模型(Bentler & Moojaart, 1989; McDonald & Marsh, 1990; Mulaik et al., 1989)。常用的衡量指标有简约基准拟合指数(Parsimony Normed Fit Index, PNFI)和简约拟合优度指数(Parsimony Goodness of Fit Index, PGFI)等,具体的评价要求见表4-16。
表4-16 整体模型拟合优度
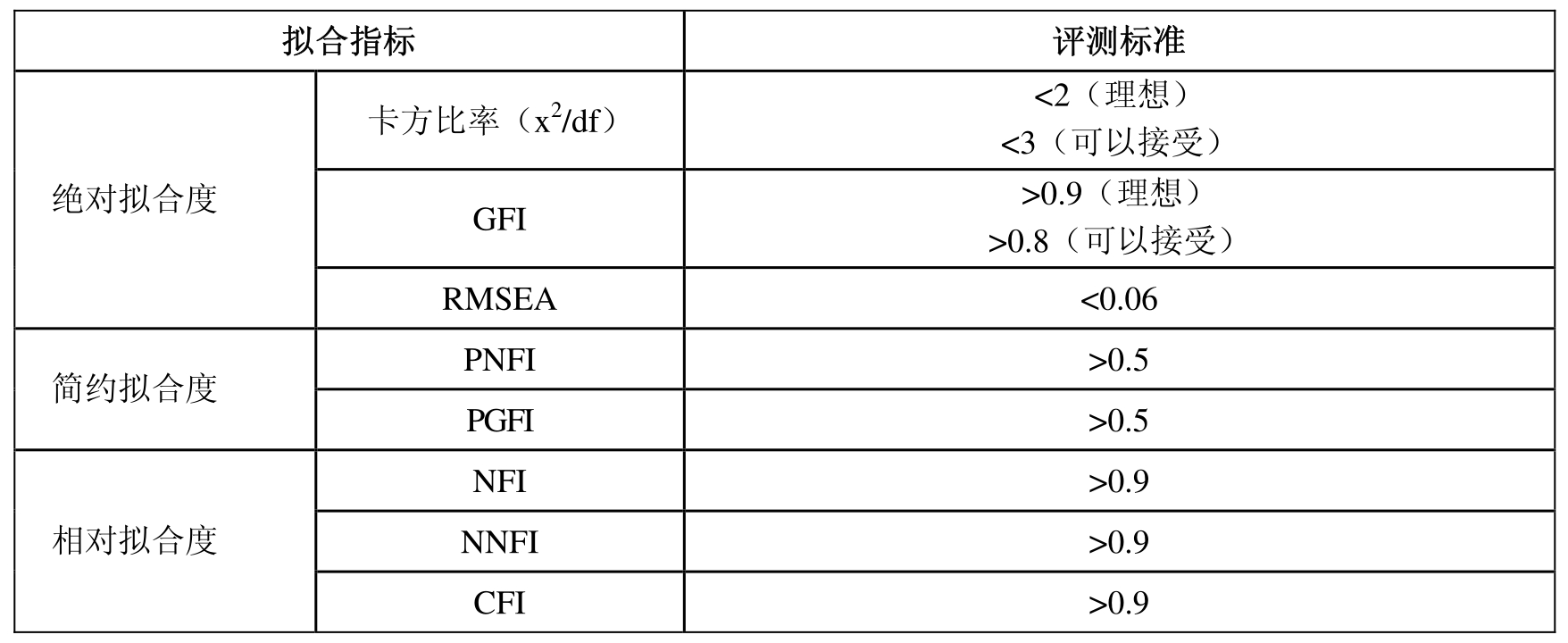
本研究将采用上述指标对所构建的理论模型进行模型的拟合检验。
3.模型内在结构拟合度
模型内在结构拟合度是用来评价模型内估计参数的显著程度、各指标和潜在变量的信度等的指标。主要包括:1.组合变量的组成信度(Composite Reliability, CR)。达到0.7以上较好,0.6为下限(Bagozzi and Yi, 1988; Fornell and Larcker, 1981)。2.平均变异抽取量(Average Variance Extracted, AVE)[27]。0.5以上为可以接受的水平。
需要说明的是,本研究将根据Anderson and Gerbing(1988)等学者的建议,采用两段法对研究模型进行分析。第一阶段,对每一个研究变量及其测量指标进行信度、效度分析,确定模型中每个研究变量的信度、效度水平。如果信度、效度的研究没有达到理想水平,则将对测量指标进行调整,直到符合理想的标准。第二阶段,将在第一阶段的基础上,将研究变量的多个测量指标缩减为少数或一个测量指标,并运用LISREL进行模型分析。