1.2.2 数制间的转换
1.2.2 数制间的转换
不同进位计数制之间的转换,实质上是基数间的转换。各数制之间进行转换时,通常对整数部分和小数部分分别进行转换,然后将其转换结果合并即可。
1.2.2.1 非十进制数转换为十进制数
非十进制数转换成十进制数的方法是:把各个非十进制数按以下求和公式展开求和即可。
![]()
式中,1a ,2a ,1ma−,ma为系数;x为基数;n为项数。
例如:
(100.101)B=1×22+0×21+0×20+1×2−1+0×2−2+1×2−3=(4.625)D
(63.56)O=6×81+3×80+5×8−1+6×8−2=(51.71875)D
(28.3C)H=2×161+8×160+3×16−1+12×16−2=(40.234375)D
1.2.2.2 十进制数转换为非十进制数
方法:整数部分采取“除X取余法”,从下往上取;
小数部分采取“乘X取整法”,从上往下取。
例如:将十进制数358.375转换为二进制数,R取2。
因为(358)D=(101100110)B,(0.375)D=(0.011)B;
所以将整数和小数合并在一起,(358.375)D=(101100110.011)B
具体步骤如表1-2所示。
表1-2 整数部分与小数部分的转换表
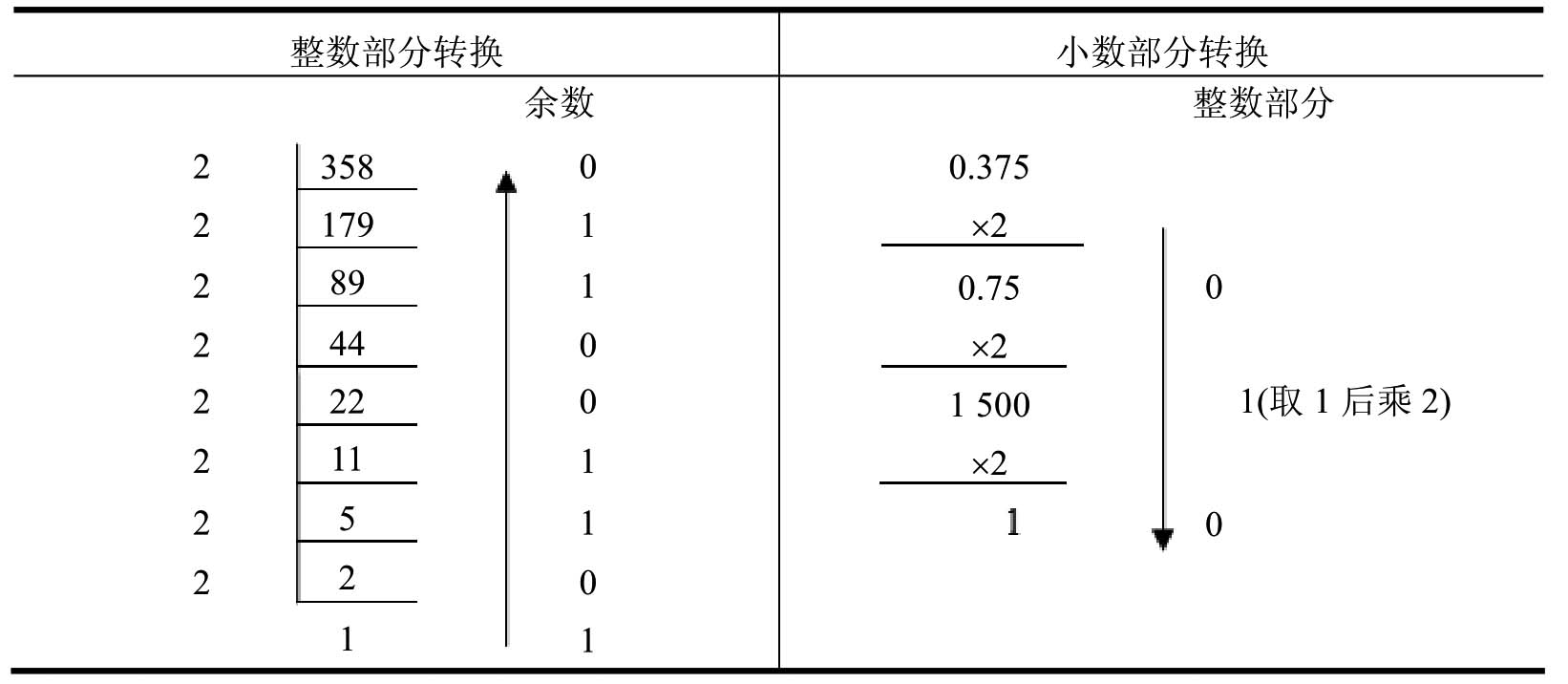
注意:十进制转换为八进制、十六进制的方法与十进制转换为二进制的方法类似。
十进制整数→八进制方法:“除8取余”;
十进制整数→十六进制方法:“除16取余”;
十进制小数→八进制小数方法:“乘8取整”;
十进制小数→十六进制小数方法:“乘16取整”。
1.2.2.3 二进制、八进制、十六进制之间的转换
1.二进制与八进制之间的转换
二进制数转换为八进制数的方法是以小数点为界,分别向左或右将每三位二进制数合成为一位八进制数即可。如果不足三位,可用零补足。
反之,八进制数转换为二进制数,将每一位八进制数展成三位二进制数即可。
例如:
10100101.11011)B=(010 100 101.110 110)B=(245.65)O
(120.45)O=(001 010 000.100 101)B
2.二进制与十六进制之间的转换
二进制数转换十六进制数的方法是以小数点为界,分别向左或右将每四位二进制数合成一位十六进制数即可。如果不足四位,可用零补足。
反之,十六进制数转换为二进制数,将每一位十六进制数展成四位二进制数即可。
例如:
(11010101.01101)B=(1101 0101.0110 1000)B=(D5.68)H
(A1D.9F)H=(1010 0001 1101.1001 1111)B
1.2.2.4 二进制的运算规则
二进制的运算有算术运算和逻辑运算两种。
◆ 算术运算:二进制数的算术运算有加法、减法、乘法和除法。
加法规则:0+0=0 0+l=l 1+0=l l+1=10
减法规则:0-0=0 l-1=0 1-0=l 10-l=l
乘法规则:0×0=0 0×1=0 l×0=0 l×1=l
除法规则:0÷0=0 0÷1=0 l÷0(无意义)l÷1=l
◆ 逻辑运算:“或”运算、“与”运算和“非”运算3种。
“或”运算规则如下:
0+0=0 0+1=1 1+0=1 1+1=1
0∨0=0 0∨1=1 1∨0=1 1∨1=1
“与”运算规则如下:
0×0=0 0×1=0 1×0=0 1×1=1
0∧0=0 0∧1=0 1∧0=0 1∧1=1
0·0=0 0·1=0 1·0=0 1·1=1
“非”运算规则如下:
![]()
虽然计算机内部均用二进制(0和1)来表示各种信息,但计算机与外部交换信息仍采用人们熟悉和便于阅读的形式,如十进制数据、文字显示以及图形描述等,其相互间的转换,则由计算机系统的硬件和软件来实现。在计算机内部,信息的表示依赖于机器硬件电路的状态,信息采用什么表示形式,将直接影响计算机的结构与性能。